Navigation in Spaaaaaace!
How do you size a rocket for a mission? This is actually not very difficult to do if you know the pertinent equations. One of the first things you need to know is where you are going. This determines your delta v, the total change in velocity that your rocket makes as it accelerates the payload. To get into orbit, for example, you need to know how fast your payload ends up going.
Circular Orbits:

The velocity at which objects orbit a planet is determined by gravity and the altitude of the orbit. Orbits can be circular, elliptical, or hyperbolic (with a boundary case of a parabolic orbit). Hyperbolic orbits are escape trajectories, or trajectories which don’t involve capture by a planet. The orbital energy in these cases is greater than the escape energy of the system.
For circular orbits, if you use Newton’s gravity and balance it with centrifugal acceleration, you can solve for the velocity which an object has to attain to orbit.
For a low earth orbit (from about 100km to 1500 km), (100 km for this example) you rotate at a rate of 7840 m/sec. This is blazingly fast – one of the reasons why it takes so much fuel to get into orbit. But this isn’t the totality of the delta v which the rocket must expend. Part of it is drag loss. The rocket ascends through the atmosphere faster than any aircraft could hope to go, and drag wastes some of your propellant, usually around 1000 m/sec or so. Gravity loss is also an issue. If your rocket didn’t produce enough thrust to overcome gravity, it would go nowhere, but expend tons of propellant, hence effective delta v loss. Delta v losses for gravity are between 500m/sec and 1000 m/sec usually. They are equal to the effective gravitational acceleration on your rocket multiplied by the amount of time that it’s burning fuel to fight it.
Altogether, about 9000 m/sec delta v is required to get into low earth orbit.
Maneuvering in space:

To go beyond low earth orbit, additional burns must be made. Gravity and drag loss don’t factor in as much (for short burns) when you are beyond earth’s atmosphere and already in orbit. If you burn in your orbital direction, you will raise your orbital eccentricity, and enter an elliptical orbit. If you burn against your orbital direction, you will enter another elliptical orbit that oscillates between where you are and a lower altitude.
One of the simplest maneuvers to raise or lower your orbital altitude is the hohman transfer. For short burns, it is also the most fuel efficient trajectory for changing orbital altitude. It involves burning once to enter an elliptical transfer orbit. You then travel from the perigee of the elliptical transfer orbit to the apogee, where you burn again in the orbital direction to circularize your orbit. Then you are at a circular orbit with a higher altitude.
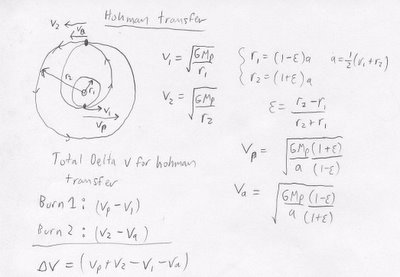
To transfer from low earth orbit to geosynchronous orbit – 35786 km – we first have to increment our velocity to get into the transfer ellipse. Our current orbital velocity is 7840 m/sec. The eccentricity of the transfer ellipse is 0.6934. The semi-major axis is 21132 km. The velocity at perigee needs to be 10201 m/sec. You have to burn to increment your orbital velocity by 2361 m/sec. Then you coast until you reach apogee, where your velocity is 1847 m/sec. The circular orbit velocity at a radius of 35786 km is 3336 m/sec. You have to burn again to increment your velocity by 1489 m/sec. The total delta v for this transfer is 3850 m/sec.
Circular Orbits:

The velocity at which objects orbit a planet is determined by gravity and the altitude of the orbit. Orbits can be circular, elliptical, or hyperbolic (with a boundary case of a parabolic orbit). Hyperbolic orbits are escape trajectories, or trajectories which don’t involve capture by a planet. The orbital energy in these cases is greater than the escape energy of the system.
For circular orbits, if you use Newton’s gravity and balance it with centrifugal acceleration, you can solve for the velocity which an object has to attain to orbit.
For a low earth orbit (from about 100km to 1500 km), (100 km for this example) you rotate at a rate of 7840 m/sec. This is blazingly fast – one of the reasons why it takes so much fuel to get into orbit. But this isn’t the totality of the delta v which the rocket must expend. Part of it is drag loss. The rocket ascends through the atmosphere faster than any aircraft could hope to go, and drag wastes some of your propellant, usually around 1000 m/sec or so. Gravity loss is also an issue. If your rocket didn’t produce enough thrust to overcome gravity, it would go nowhere, but expend tons of propellant, hence effective delta v loss. Delta v losses for gravity are between 500m/sec and 1000 m/sec usually. They are equal to the effective gravitational acceleration on your rocket multiplied by the amount of time that it’s burning fuel to fight it.
Altogether, about 9000 m/sec delta v is required to get into low earth orbit.
Maneuvering in space:

To go beyond low earth orbit, additional burns must be made. Gravity and drag loss don’t factor in as much (for short burns) when you are beyond earth’s atmosphere and already in orbit. If you burn in your orbital direction, you will raise your orbital eccentricity, and enter an elliptical orbit. If you burn against your orbital direction, you will enter another elliptical orbit that oscillates between where you are and a lower altitude.
One of the simplest maneuvers to raise or lower your orbital altitude is the hohman transfer. For short burns, it is also the most fuel efficient trajectory for changing orbital altitude. It involves burning once to enter an elliptical transfer orbit. You then travel from the perigee of the elliptical transfer orbit to the apogee, where you burn again in the orbital direction to circularize your orbit. Then you are at a circular orbit with a higher altitude.

To transfer from low earth orbit to geosynchronous orbit – 35786 km – we first have to increment our velocity to get into the transfer ellipse. Our current orbital velocity is 7840 m/sec. The eccentricity of the transfer ellipse is 0.6934. The semi-major axis is 21132 km. The velocity at perigee needs to be 10201 m/sec. You have to burn to increment your orbital velocity by 2361 m/sec. Then you coast until you reach apogee, where your velocity is 1847 m/sec. The circular orbit velocity at a radius of 35786 km is 3336 m/sec. You have to burn again to increment your velocity by 1489 m/sec. The total delta v for this transfer is 3850 m/sec.


0 Comments:
Post a Comment
<< Home